Электромагнитные волны

Кратко:
Ошибочные представления об электромагнитных взаимодействиях привели к ряду парадоксальных выводов о природе электромагнитных волн. Распространение электромагнитных волн возможно лишь в материальной среде, содержащей электрические заряды. Предполагается, что «электромагнитное излучение» — это процесс переноса электрической энергии в физическом вакууме.

Догадываюсь, что у заинтересованного читателя уже давно готов вопрос: «Вот вы развенчали максвелловскую форму представления электромагнитной индукции, отказали в праве на жизнь вихревому электрическому полю… Но как же быть с электромагнитными волнами? Ведь они-то существуют!».

Вопрос законный — сегодня в существовании электромагнитного излучения не сомневаются даже те, кто считает, что на всё воля божья. На этой страничке я и хочу поговорить, наконец, об электромагнитных волнах.

О системе уравнений электродинамики

Представления о природе электромагнитных волн (ЭМВ) заложены в систему уравнений, составляющую основу современной электродинамики. Эта теория разрабатывалась Дж. Максвеллом почти два десятилетия (с 1855 по 1873 годы), и в дальнейшем неоднократно правилась и преобразовывалась другими исследователями — Г. Герцем, О. Хевисайдом, А. Эйнштейном, Г. Лоренцем и другими. Существенным правкам подверглись не только уравнения, но и некоторые идеи Максвелла. Приведу лишь один вывод из сборника статей, посвященного 150-летию со дня рождения Максвелла:

Общеупотребительная ныне система уравнений Максвелла не соответствует ни одной из систем, данных в работах Д. К. Максвелла¹.

Вывод о существовании ЭМВ и электромагнитной природе света является основным следствием из теории Максвелла. Сегодня трудно говорить о деталях его творческого метода. Поэтому многие высказывания о ходе мыслей Максвелла сегодня являются не более чем предположениями. Позволю себе тоже сделать одно предположение. Мне кажется, что мысль о существовании электромагнитных волн не стала следствием, а предшествовала разработке системы уравнений электродинамики, и даже больше — была одной из целей этой работы. Ещё в декабре 1861 года в письме к У. Томсону (Кельвину) Максвелл высказал предположение, что «…магнитная и светоносная среды идентичны». Есть документальные свидетельства, подтверждающие, что о существовании ЭМВ догадывался ещё Фарадей.

К середине XIX века все основные законы электродинамики были уже известны: закон Био-Савара и Ампера были открыты в 1820 году, в 1831 году Фарадей получил основной закон электромагнитной индукции, а в 1839 году Карл Гаусс сформулировал основную теорему электростатики — теорему Гаусса-Остроградского. Максвелл обобщил эти зависимости, сведя их в единую систему уравнений. Эта система состоит из семи уравнений, но основу системы составляют два уравнения:

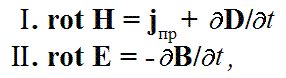
которые описывают взаимные превращения электрического поля в магнитное (I) и наоборот (II).

На разработку этой системы Максвеллу — талантливому физику-теоретику, автору блестящих работ по молекулярной физике, механике, оптике — потребовалось почти двадцать лет! Объяснить это можно лишь тем, что при разработке системы уравнений электродинамики он столкнулся с огромными трудностями, не связанными с математикой. Основная трудность заключалась в том, что Максвелл опередил свое время: он остро ощущал дефицит знаний, необходимых для понимания физики (природы) электромагнитных взаимодействий.

Процесс генерации и распространения электромагнитных волн требовал симметрии взаимопревращений электрической и магнитной компонент волны. Так появилась максвелловская формула закона электромагнитной индукции, которая получила свое отражение во II уравнении системы (1).

Электромагнитные волны. Фазовые соотношения в ЭМВ

Решение системы уравнений электродинамики приводит к волновым дифференциальным уравнениям — для напряженностей электрического (E ) и магнитного (H ) полей:

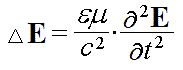
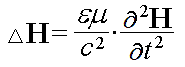
Эти уравнения дают для E и H два одинаковых волновых решения. Электрическая и магнитная волны лежат во взаимно перпендикулярных плоскостях и синфазны. Этот результат приводится во всех учебниках и пособиях по электродинамике. Но если компоненты электромагнитной волны синфазны, то возникает коварный вопрос: а возможно ли вообще существование электромагнитных волн? Ведь распространение колебаний в пространстве возможно лишь в том случае, когда существует механизм передачи возбуждения (энергии колебаний) из одной точки среды в соседнюю точку. В упругих средах этот механизм обусловлен упругостью (взаимодействием молекул) среды. В вакууме механизмом «близкодействия» может быть лишь переход энергии электрических колебаний в энергию магнитных колебаний в соседней точке пространства и наоборот. В этом заключалась основная идея Максвелла, которая привела его к мысли о существовании электромагнитных волн! Но если колебания синфазны, то такое электромагнитное «зацепление» между точками пространства отсутствует, что исключает возможность распространения электромагнитных колебаний. То есть, синфазная электромагнитная волна не может быть бегущей.

Для электромагнитного излучения в замкнутой области (например, для стоячих волн в резонаторе) уравнения Максвелла дают между компонентами ЭМВ сдвиг в четверть периода². При этом одна из компонент волны должна иметь на стенках резонатора пучность, что невозможно, так как стенки резонатора непрозрачны для электромагнитного поля. Кроме того, электромагнитная энергия (не отдельных компонентов, а полная энергия волны!) в такой стоячей волне совершает колебания на отрезке в четверть волны, что также не характерно для стоячих волн.

Таким образом, строгий физический анализ решений современной системы уравнений электродинамики приводит к странным выводам, что бегущая электромагнитная волна не может «бежать», а стоячая волна не хочет «стоять»!

Далее. Если электрическая и магнитная компоненты ЭМВ синфазны, то в любой точке волнового пространства электрическая и магнитная энергия не переходят друг в друга, а возникают, растут и исчезают одновременно. При этом плотность потока электромагнитной энергии (модуль вектора Умова-Пойнтинга) пульсирует по гармоническому закону. Не нарушается ли здесь закон сохранения энергии?

Наконец, синфазность компонентов в электромагнитной волне противоречит самой максвелловской формулировке основного закона электромагнитной индукции, согласно которой напряжённость электрического поля должна быть пропорциональна производной от магнитной индукции.

Любого из этих аргументов достаточно, чтобы заключить, что не все благополучно в максвелловом королевстве. Но сторонники современной интерпретации природы электромагнитных волн старательно не замечают этот физический парадокс. Менее уверены в правильности такого решения специалисты-практики. Например, автор³ убежден, что «колебания магнитного поля опережают колебания электрического поля на π/2 ». С этим согласны и другие специалисты по электросвязи. Существуют и эксперименты, подтверждающие эту точку зрения (см.⁴). Но ни те, ни другие не могут объяснить причину этого парадокса.

Ток смещения

Современные представления о природе ЭМВ сводятся к тому, что переменное вихревое магнитное поле создаёт нестационарное вихревое электрическое поле, перпендикулярное магнитному. В свою очередь электрическое поле генерирует вихревое магнитное поле и т.д. Но со времен Х. Эрстеда и экспериментов Био и Савара известно, что магнитное поле создаётся электрическим током!

Исключение электрических зарядов и токов из процесса электромагнитной индукции стало для Максвелла камнем преткновения при разработке системы уравнений электродинамики. Если бы Максвелл творил в наше время, то эту систему ему вряд ли удалось написать, потому что совершенно неразрешимой показалась бы задача объяснить распространение ЭМВ в вакууме. Но во времена Максвелла считалось, что все пространство заполнено мировым эфиром, обладающим весьма неопределенными свойствами.

В 1837 году М. Фарадей обнаружил явление поляризации диэлектриков в электрическом поле и высказал мысль о возможности распространения «электрического и магнитного действия» через промежуточную материальную среду. В 1861 году, анализируя поведение диэлектрика в электрическом поле, Максвелл предположил, что взаимное смещение зарядов в молекулах диэлектрика пропорционально напряженности внешнего электрического поля E . В современных обозначениях эта зависимость определяет электрическую индукцию D = ε₀E , где ε₀ — электрическая постоянная. При изменении электрического поля в диэлектрике кратковременно протекает ток (ток поляризации), плотность которого определяется зависимостью j_см = dD/dt = ε₀dE/dt . Этот ток Максвелл назвал «током смещения». Это был, хоть и кратковременный, но ток реальных зарядов, который должен был создавать магнитное поле. Это позволяло объединить плотность тока смещения j_см с плотностью тока проводимости j_пр в общий («полный») ток. Суммарную плотность полного тока Максвелл и включил в I уравнение системы (1).

Цитирую по⁵:

Следует помнить, что вакуум в смысле электромагнитной теории есть понятие чуждое Максвеллу, так что диэлектрик включает и тот случай, который мы бы описали как пустое пространство.

Для Максвелла «мировой эфир» не был «пустым пространством». Он полагал, что эфир, как и диэлектрик, содержит связанные электрические заряды. Таким образом, исключив заряды из закона электромагнитной индукции (II уравнение), Максвелл вынужден был ввести их в процесс распространения ЭМВ. В то время это был единственный разумный выход, позволявший сохранить идею существования электромагнитных волн. Но для этого потребовалось наделить мировой эфир свойствами диэлектрика…

На грани веков, когда создавалась теория относительности, с первым уравнением Максвелла начали происходить чудеса. Постулаты теории относительности исключали существование мирового эфира. Это понятие было безжалостно изгнано из научного обихода. Вместе с эфиром на свалку научных отбросов выплеснули и ребенка — идею Фарадея о неразрывной связи электрического поля с электрическими зарядами. Казалось бы, с исчезновением эфира должна была обрушиться вся система рассуждений, положенная Максвеллом в основу электродинамики. Но релятивисты, не решаясь обидеть ни Максвелла, ни Эйнштейна, изобрели вихревое электрическое поле. Это была «гениальная» находка, так как она избавляла индукционный процесс (а, следовательно, и ЭМВ) вообще от всяких зарядов! В пустоте не могло быть тока проводимости, поэтому первое уравнение получило форму

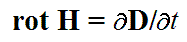
Таким образом, магнитное поле в ЭМВ создавалось теперь только «полем электрического смещения». Авторы этой идеи не заметили, что электрические заряды присутствуют и в параметре D , так как по своему физическому смыслу электрическая индукция представляет собой поверхностную плотность зарядов, возникающую в диэлектрике в процессе поляризации. Без зарядов переменное электрическое поле не может ни поляризовать пустоту, ни создавать ток смещения. Отсутствующие в вакууме молекулы заменили несуществующим «вихревым электрическим полем», а производную от этого фантома назвали «током смещения в вакууме».

Во II томе Берклиевского курса физики⁶ Э. Парсел приводит любопытный анализ тока смещения в вакуумном конденсаторе. Он показывает, что ток смещения в вакууме магнитное поле… не создаёт. Напряженность магнитного поля в любой точке пространства внутри и вне конденсатора определяется суперпозицией полей от двух «полутоков» проводимости — втекающего в одну пластину конденсатора и вытекающего из другой⁷.

Сторонники непорочности системы уравнений Максвелла утверждают, что способность изменяющегося электрического поля создавать в вакууме ток смещения без участия зарядов — это эффект релятивистский, а производную dD/dt называют «релятивистской поправкой». Вводя в систему уравнений понятие «ток смещения», Максвелл об этом не догадывался…

О природе электромагнитных волн

Электромагнитные волны — это венец системы уравнений электродинамики, очень важный для практики, сложный и плохо изученный природный процесс. Ошибочные представления об электрической энергии и её формах и путаница в процессах генерации и расходования электроэнергии привели к ряду утверждений о природе ЭМВ, которые полны противоречий.

Как же сегодня представляется природа ЭМВ в официальной электродинамике? Энергия (несуществующего) «вихревого электрического поля» поочередно переходит в ещё менее определенное понятие — «энергию магнитного поля» и наоборот. Так как оба поля синфазны, то все это происходит в одной точке. Магнитное поле создаётся (отсутствующим в вакууме) «током смещения», а «поток электромагнитной энергии» непрерывно пульсирует, то исчезая, то возникая вновь. Этот фантазийный винегрет и называется сегодня «электромагнитным излучением». Если же правы некоторые уважаемые авторы, что реально только электрическое поле, а магнитное поле — «не более чем удобный прием» для описания электродинамических взаимодействий, то электромагнитные волны вообще зависают в вакууме, как птица с одним крылом!

Я не тешу себя иллюзиями, что смогу вскрыть и объяснить природу электромагнитного излучения. Попытаюсь лишь предложить возможный механизм образования и распространения электромагнитных волн, свободный от этих нелепостей.

Сторонние силы в ЭМВ

Нет необходимости доказывать, что электромагнитная индукция имеет непосредственное отношение к образованию и распространению ЭМВ. Один из двух процессов взаимопревращений в ЭМВ — это процесс генерации электрической энергии из энергии магнитной. Этот процесс требует участия электрических зарядов и сторонних сил.

Вакуум не является проводящей средой и не содержит свободных зарядов. Поэтому единственным током, генерирующим магнитное поле в ЭМВ, может быть только ток смещения. Но это не тот иллюзорный ток, который возникает при дифференцировании «вихревого электрического поля», а ток смещения реальных зарядов, как его понимал Максвелл — ток поляризации мирового эфира. Отсюда следует, что для существования ЭМВ в «пустом» пространстве должны существовать связанные электрические заряды противоположного знака. Это и есть тот единственный постулат, который Максвелл положил в основу всей системы уравнений электродинамики, и чего упорно не желают замечать его адепты.

Рассуждать о природе этих электронейтральных образований бессмысленно — сегодня о них можно сказать лишь, что они существуют и как-то заполняют «пустое» пространство. Известно, например, реально существующее (обнаруженное экспериментально) электронейтральное образование — позитроний. «Атом» позитрония представляет собой водородоподобную связь электрона с позитроном. Имеет ли позитроний какое-либо отношение к «атомам эфира», ещё предстоит выяснить. В дальнейшем мы будем называть их «позитронием» лишь для краткости.

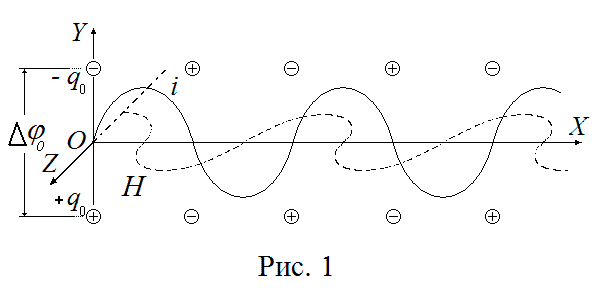
Допустим, в некоторой плоскости пространства YОZ появляется возмущение, которое выражается в том, что заряды «позитрония» оказываются разнесенными на некоторое расстояние (Рис. 1). В неподвижности система двух разнесенных зарядов обладает потенциальной электрической энергией qΔφ₀ , где q — заряд одного знака, а Δφ₀ — разность потенциалов между полюсами диполя. Если предоставить систему самой себе, электрические заряды начнут ускоряться навстречу друг другу, а «энергия положения» будет переходить в «энергию движения» электрических зарядов — энергию электрического тока. Если потенциальная энергия связанных зарядов будет изменяться по гармоническому закону, то разность потенциалов в этом месте будет описываться, допустим, функцией

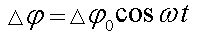
Как и в гармонических индукционных процессах генерации, электрический ток, возникающий при сближении зарядов, будет отставать от Δφ на π/2 . Тогда плотность этого тока можно выразить соотношением:

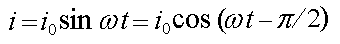
Если обратиться к механизму распространения волн (например, механических), то можно предположить, что на следующем этапе должна произойти передача «энергии движения» в соседнюю точку пространства. Природа этого процесса сегодня неизвестна. Согласно существующим представлениям передача энергии в ЭМВ осуществляется посредством магнитного поля. Эта модель используется в электродинамике уже более 100 лет и даёт правильные результаты — как качественные, так и количественные, что позволяет использовать её и в наших рассуждениях.

Согласно электромагнитной модели распространения ЭМВ ток смещения создаёт в плоскости, перпендикулярной току, магнитное поле, распространяющееся в пространстве в виде волны напряженности магнитного поля H .

В соответствии с законом электромагнитной индукции Фарадея магнитный поток (а, следовательно, и напряжённость магнитного поля) отстает по фазе от индукционного тока на π/2 . То же следует и из диаграмм, описывающих гармонический индукционный процесс. Осцилляции атомов «позитрония» можно рассматривать, как колебания тока в «микрогенераторе» (тока смещения), с той разницей, что в вакууме «энергия движения» не рассеивается, а целиком переходит в потенциальную энергию. Таким образом, для магнитной напряженности в начальной плоскости, создаваемой током смещения, можно записать соотношение

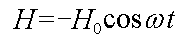
что создаёт плоскую «магнитную волну» в направлении оси X , поляризованную в плоскости XOZ :

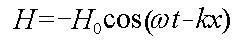
По индукционному механизму «магнитная волна» создаёт волну плотности индукционного тока (тока смещения), опережающую её на четверть волны:

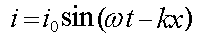
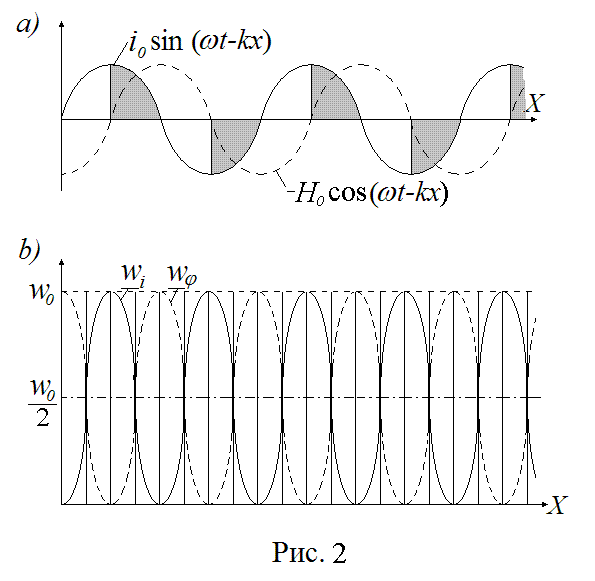
На Рис. 2а (без учета плоскостей поляризации волн) пунктиром приведена волна магнитной напряженности (6) и волна плотности тока смещения (7) (контурная кривая).

По аналогии с током в разомкнутом «микрогенераторе», ток смещения складывается из стороннего i (индукционного) и потенциального i' тока (аналог тока проводимости), являющегося продолжением стороннего тока. Сторонний и потенциальный токи сменяют друг друга каждую четверть периода.

Разность потенциалов, создаваемая сторонним током, играет здесь роль обратной ЭДС Э_i . Как и в разомкнутом «микрогенераторе», она опережает индукционный ток по фазе на π/2 и образует волну, опережающую ток смещения на четверть волны:

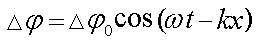
Сторонние силы приводят к поляризации вакуума, а потенциальные создают пульсирующий ток. Участки волны плотности тока, на которых работают сторонние силы, на Рис. 2а затенены. На этих участках происходит генерация потенциальной электрической энергии.

Сторонними силами в данном рассмотрении следует считать «магнитные силы». На светлых участках происходит превращение потенциальной энергии в электрическую «энергию движения».

Энергия ЭМВ

Потенциальная электрическая энергия определяется соотношением W_φ = qΔφ . Так как q ~ Δφ , то можно считать, что плотность потенциальной энергии в плоскости YОZ (с учётом (3)) изменяется со временем по закону

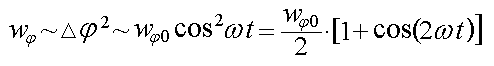
где w_φ0 ~ q₀Δφ₀ . Эта зависимость представляет косинусоиду с удвоенной частотой (2ωt ), приподнятую над осью абсцисс на половину амплитуды (w_φ0 / 2 ) (см. Рис. 2b).

Плотность «электрической энергии движения» пропорциональна квадрату плотности тока смещения: w_i0 ~ i² . Поэтому колебания энергии тока смещения в плоскости YОZ будут определяться с учётом (4) зависимостью

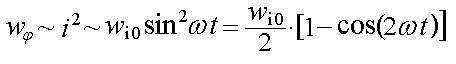
где

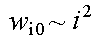
На Рис. 2b плотности потенциальной энергии w_φ — (9) и «энергии движения» w_i0 — (10) представлены волнами, распространяющимися в направлении оси X . Если отсутствуют потери энергии, то каждые четверть периода потенциальная энергия целиком переходит в «энергию движения». В любой точке волнового пространства плотность электрической энергии равна w_φ0 = w_i0 = w_φ + w_i = w₀ = const . Это значит, что плотность потока энергии (модуль вектора Умова-Пойнтинга) w₀c = const , то есть в любой точке плоской волны со временем не меняется (c — фазовая скорость волны).

Таким образом, то, что мы сегодня называем «электромагнитными волнами», согласно данному предположению представляет собой волны электрической энергии. Распространение этих волн обусловлено процессом перехода электрической энергии из потенциальной формы в «энергию движения» (энергию электрического тока) и обратно.

Механизмом, связывающим соседние точки пространства и обеспечивающим движение электрических волн, следует сегодня считать модель с участием магнитного поля, с той особенностью, что магнитное поле, не обладая собственной энергией, выполняет в этом процессе лишь роль посредника, передающего электрическую «энергию движения» в соседнюю точку пространства. Вопрос о физической природе «электрической упругости» физического вакуума остаётся открытым. Понять природу этого процесса можно будет лишь тогда, когда определится структура физического вакуума. Например, автор⁸ считает, что вакуум состоит из перемежающихся положительных и отрицательных зарядов, образующих кубическую структуру, подобную структуре NaCl. В такой модели передача «энергии движения» в соседнюю точку пространства будет происходить в результате обычного кулоновского взаимодействия разноименных зарядов в смежных «ячейках» вакуумной структуры.

• Назад: Гармонические индукционные процессы
• Далее: Результаты, выводы и немного морали

Комментарии

Вы можете добавить свой комментарий. Пожалуйста, оставляйте только комментарии по теме данной страницы.