Электрическая энергия

Кратко:
Превращение различных видов энергии в электрическую выполняют сторонние силы, перемещающие электрические заряды против сил электрического поля. Типичная ошибка многих исследований — отождествление сторонних и потенциальных сил. Электрическая энергия имеет две разновидности: потенциальную и кинетическую.

Самый большой вред теория «взаимодействия полей» нанесла понятию электрическая энергия. Чтобы всё вернуть на свои места, потребуется, по-видимому, не одно десятилетие. И начать придётся с исходных представлений творцов классической электродинамики, учитывая рациональные результаты последующих исследований.

Сторонние силы и их свойства

Любая замкнутая электрическая цепь для покрытия тепловых (и других) энергетических потерь должна включать устройство, воспроизводящее электрическую энергию из других видов энергии — электрогенератор. За полтора века практического использования электроэнергии создано много электрогенераторов разных типов, конструкций и параметров. На этой странице мы будем говорить лишь о генераторах постоянного тока.

Общим для всех электрогенераторов является принцип преобразования различных видов энергии в электрическую. Он заключается в разделении электрических зарядов противоположного знака и разведении их на некоторое (межэлектродное) расстояние. При этом электроэнергия, выработанная генератором, выступает в форме потенциальной электрической энергии — разности потенциалов на его выходных клеммах (электродах) — ЭДС генератора.

Чтобы преодолеть кулоновское притяжение между зарядами противоположного знака, нужны силы. Академик И. Е. Тамм¹ предложил называть их сторонними силами.

Понятие «сторонние силы» — это некоторая абстракция, которая обозначает силы разной природы, выполняющие одну и ту же функцию — преобразование различных видов энергии в энергию электрическую. Смысл этого нового понятия, его физическое содержание необходимо было бы чётко определить. К сожалению, И. Е. Тамм этого не сделал. Попытаемся восполнить это упущение.

Главной задачей сторонних сил является генерация электрической энергии, то есть превращение энергии различной природы (механической, химической, тепловой, оптической и пр.) в электрическую. Эта задача решается путём перемещения электрически заряженных частиц против сил электростатического поля. Отсюда — главное свойство, заложенное И. Е. Таммом в название «сторонние силы»:

1. Природа сторонних сил может быть самой разной, но она должна быть «сторонней» — не электростатической. Отсюда следует, что
2. Сторонние силы не действуют на электрический заряд. В зависимости от их физической природы сторонние силы могут действовать на другие свойства заряженных частиц — массу, форму, размер, плотность, их коллективные свойства — концентрацию и пр.
3. Подавляющее большинство сторонних сил имеет не «полевой» характер. Поэтому описывать действие этих сил как проявление некоторого «поля сторонних сил» нежелательно. Если это представление всё же используется, то необходимо учитывать, что «пробными телами» в этих «полях» служат не электрические, а другие «заряды» (см. поясняющий текст к формуле (1)).
4. Действие сторонних сил всегда сопровождается генерацией электрической энергии — образованием разности потенциалов на некоторых разнесённых (проводящих) телах — «клеммах» генератора, на которых электрические заряды концентрируются. Поэтому
5. Сторонние силы «работают» лишь внутри генератора. Вне генератора на заряженные частицы действуют электростатические (потенциальные) силы.

Примечание: поскольку сторонними силами бывают силы разной природы, то те же силы могут участвовать в различных процессах, не имеющих никакого отношения к генерации электроэнергии. То есть название «сторонняя сила» характеризует не столько физическую природу силы, сколько её функциональное назначение. Это понятие правильнее было бы определить так:

Сторонними силами называются силы не электростатической природы, участвующие в создании электрической энергии.

Генератор постоянного тока

Я понимаю, что некоторые из приведенных выше утверждений могут вызвать у читателей удивление (возможно, даже возмущение). Так как именно среди таких читателей я надеюсь найти единомышленников, то напомню нетерпеливым, что всё сказанное относится к генераторам постоянного тока. К индукционным процессам мы обратимся позднее.

Рассмотрим несколько подробнее работу сторонних сил в абстрактном идеальном генераторе постоянного тока. Природа сторонних сил в таком генераторе может быть любой (в этом — смысл определения абстрактный), но они должны обладать всеми перечисленными выше свойствами. Идеальным мы называем генератор, не имеющий внутреннего сопротивления. При перемещении заряженных частиц в таком генераторе тепловые потери отсутствуют.

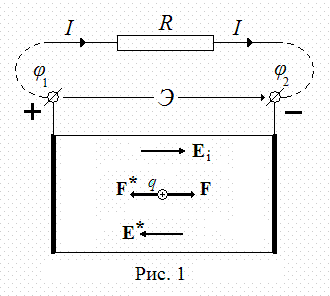
Положим, на всем пути между электродами на частицу, несущую положительный электрический заряд q , действует постоянная сторонняя сила F^* (Рис. 1). Величина этой силы определяется её природой и не зависит от электрического заряда частицы. Такую силу можно условно представить как результат воздействия на частицу удельной силы E^* — «напряженности» некоторого «поля сторонних сил», отнесённой к единице электрического заряда частицы:

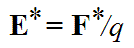
Допустим, что в тот момент, когда включаются сторонние силы, генератор «разряжен». Под действием этих сил положительно заряженные частицы устремляются к положительному электроду генератора, а отрицательные частицы — к противоположному полюсу. По мере того, как на электродах накапливаются заряды противоположного знака, возрастает разность потенциалов на выходных клеммах генератора. Одновременно растет и внутреннее электрическое (потенциальное) поле E_i , направленное против сторонних сил. Когда сила воздействия этого поля на единицу электрического заряда частицы достигает (по модулю) силы F^* «стороннего поля» (F_i = -F^* ), наступает равновесие E_i = -E^* , и направленное движение заряженных частиц прекращается. На клеммах генератора устанавливается разность потенциалов Δφ = φ₁ — φ₂ = Э , которая и определяет ЭДС генератора, максимально возможную при данном способе генерации. Численно она равна работе, затрачиваемой сторонними силами на перемещение единицы электрического заряда внутри генератора.

Если клеммы генератора замкнуть на нагрузку R (см. пунктир на Рис. 1), по цепи потечет постоянный ток I = Э/R и движение заряженных частиц в генераторе возобновится. Такой (рабочий) режим работы электрогенератора является квазистационарным: поступающие на электрод заряды компенсируют их уход во внешнюю цепь. При этом количество зарядов на электродах (а, следовательно, — и разность потенциалов) остаётся неизменным. Со временем не изменяются значения Э , E_i , сохраняется динамическое равенство F_i = -F^* , а заряженные частицы в объёме генератора движутся равномерно («по инерции»). Подчеркнём, что этот режим работы генератора, как и режим холостого хода (при разомкнутой внешней цепи) — стационарный.

В реальном генераторе внутреннее сопротивление r^* > 0 . В рабочем режиме движение заряженных частиц в генераторе остаётся равномерным, но сторонние силы немного превышают силы электростатические — на величину сил сопротивления движению частиц внутри генератора. При этом разность потенциалов на внешней цепи (напряжение на клеммах генератора) оказывается меньше его ЭДС на величину Ir^* — падение напряжения внутри генератора.

Следует заметить, однако, что «внутреннее сопротивление» r^* не является электрическим сопротивлением в том же смысле, что и внешнее сопротивление R . Дело в том, что «падение напряжения» внутри генератора — это энергетические потери источника сторонних сил. Оно лишь численно равно удельным (на единицу электрического заряда) диссипативным потерям «сторонней» энергии. Однако, поскольку силы, действующие на заряженную частицу, не воздействуют на её электрический заряд, тепловые потери не зависят от заряда частицы. Сопротивление r^* — это лишь некоторое эффективное значение, характеризующее внутренние потери энергии источника сторонних сил.

Чтобы показать, что ток внутри генератора («сторонний» ток) и ток во внешней цепи (потенциальный ток) имеют разную природу, мы сравнили эффективное сопротивление источника тока r^* с внутренним сопротивлением этого же источника r при протекании через него обратного (потенциального) тока.

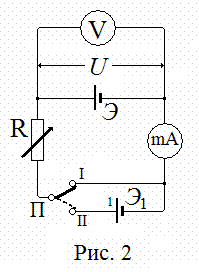
На Рис. 2 приведена принципиальная схема этих измерений. Падение напряжения U на испытуемом источнике питания измерялось высокоомным вольтметром V , а ток в цепи — миллиамперметром mA . Нагрузкой служил магазин сопротивлений R .

В положении I переключателя П измерялся прямой ток от источника питания. По показаниям приборов рассчитывалось эффективное сопротивление источника r^* = U/I . Затем в положении II переключателя навстречу ЭДС Э источника включалась ЭДС Э₁ > Э . Измерялся обратный ток I₁ , по величине которого и падению напряжения U₁ на источнике рассчитывалось истинное («электрическое») сопротивление источника r . ЭДС источника измерялась непосредственно перед этим измерением и после него и учитывалась в расчетах.

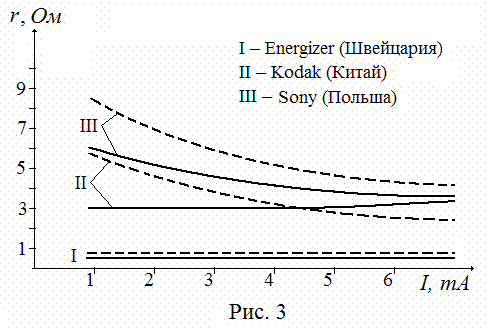
Измерения проводились на 1,5-вольтовых батарейках для карманного фонарика. На Рис. 3 приведены результаты измерений эффективного «прямого» сопротивления r^* (пунктирная кривая) и истинного «обратного» r (контурная кривая) внутреннего сопротивления для трех батареек разного производства.

Изучение стабильности внутреннего сопротивления источников, формы этих зависимостей и прочие вопросы оставим специалистам-физхимикам (электрохимикам). Но приведенные экспериментальные результаты убедительно показывают, что природа прямого («стороннего») и обратного («потенциального») токов в электрохимических генераторах различна.

«Обобщённый закон Ома»

В своем классическом труде «Основы теории электричества» И. Е. Тамм так сформулировал понятие сторонних сил:

…помимо электрических сил стационарного электрического поля на электрические заряды в проводниках может действовать ещё некоторое поле сил не электростатического происхождения…¹

С учётом свойств сторонних сил, сформулированных выше, в этом определении есть три неточности, выделенные жирным:

1. сторонние силы не действуют на электрические заряды (см. свойство 2);
2. эти силы далеко не всегда образуют поле сил (свойство 3);
3. в цепях постоянного тока сторонние силы работают не в проводниках, а только в генераторах (свойство 5).

В дальнейшем эти неточности стали причиной ошибок в использовании понятия «сторонние силы». В частности, был получен несуществующий «Обобщённый закон Ома». Основываясь на приведенном определении сторонних сил, И. Е. Тамм записал дифференциальное соотношение, определяющее плотность тока

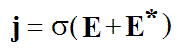
который возникает при совместном действии двух полей — электростатического E и «поля сторонних сил» E^* (σ — электропроводность среды). В этом выражении потенциальные и сторонние силы выступают как бы «на равных», то есть не учитывается основная особенность сторонних сил — их способность не только перемещать заряженные частицы, но и создавать (генерировать) электрическое поле. При выводе дифференциального соотношения (2) эта оплошность осталась незамеченной, так как оно записывалось для бесконечной однородной проводящей среды. В этом случае отсутствуют границы (области), на которых могут накапливаться электрические заряды и, следовательно, не создаётся потенциальное противополе. Ситуация кардинально меняется, когда это соотношение используется для последующего интегрирования в ограниченной области пространства. При этом генерируется обратная ЭДС E_i = -E^* , и выражение (2) превращается в j = σE — дифференциальную форму обычного закона Ома.

В отсутствии обратной ЭДС интегрирование (2) привело к соотношению

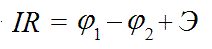
которое автор назвал «наиболее общей формой обобщенного закона Ома».

Считается, что этот закон справедлив для «неоднородного участка» цепи, содержащего электрогенератор с ЭДС Э и омическое сопротивление R (Рис. 4). I — ток, протекающий по участку, а φ₁ — φ₂ — разность потенциалов на границах участка.

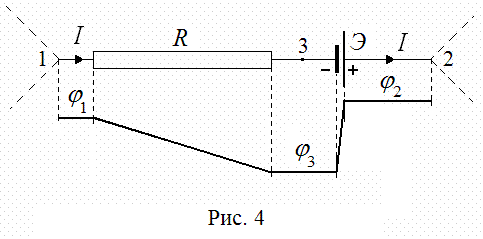
Из потенциальной диаграммы, приведенной на рисунке, следует очевидное соотношение

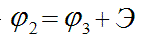
где φ₃ — потенциал на отрицательной клемме генератора. Подставляя это соотношение в (3), получаем

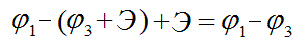
и далее IR = φ₁ - φ₂ , что является… обычным законом Ома для участка цепи. Если этот участок замкнуть, то φ₁ = φ₂ и соотношение (3) даёт закон Ома для замкнутой цепи.

Таким образом, «Обобщённый закон Ома» представляет собой лишь запутанную и необоснованно усложненную модификацию обычного (классического) закона. Этого следовало ожидать: попытка включить сторонние силы в число движущих в цепях постоянного тока не может привести к какому-либо обобщению закона Ома. Сторонние и потенциальные силы выполняют в электрических цепях прямо противоположные функции: сторонние силы создают электрическую энергию из других видов энергии, а потенциальные — расходуют эту энергию, превращая её в работу, тепло, световую энергию и пр. Закон Ома описывает только процесс диссипации (расходования) электроэнергии. Он не имеет никакого отношения к процессу генерации и не может включать в себя параметры электрогенератора.

«Обобщённый закон Ома» был получен И. Е. Таммом в 1929 году. Он присутствовал уже в первом издании «Основ теории электричества». В 50-х годах прошлого века этот «закон» вошел в справочную и учебную литературу и был включен в рабочие программы курса общей физики для разных вузов страны. Сегодня его излагают на лекциях, а студенты до сих пор решают задачки на применение «Обобщенного закона Ома» на «неоднородных участках» электрических цепей…

В основе неточностей, допущенных академиком И. Е. Таммом при выводе «Обобщенного закона Ома», лежит, как ни странно, та же ошибка, которую допустил Максвелл, представив основной закон электромагнитной индукции в форме взаимодействия полей. Действительно: по мысли Максвелла переменное поле создаёт (генерирует) индукционную ЭДС, которая в свою очередь вызывает электрический («индукционный») ток. Но мы видели, что процесс генерации ЭДС начинается с работы сторонних сил, создающих сторонний ток. ЭДС генератора является следствием работы этого тока как результат накопления зарядов на клеммах генератора. Такой механизм ЭМИ полностью соответствует экспериментам Фарадея и механизму электромагнитной индукции по методу пересечения.

Это легко понять — во времена Максвелла не было ещё чётких представлений о процессе получения электрической энергии. Но эта ошибка оказалась чрезвычайно живучей: через 100 лет эту же ошибку повторил и основатель отечественной электродинамики, автор плодотворной идеи «сторонних сил» академик И. Е. Тамм.

Но и это не всё: та же ошибка совершается, например, и при попытке отождествить сторонние силы в индукционных процессах с силой Лоренца. Мы видели, что сила Лоренца не может быть сторонней силой, так как она не может передать заряду энергию. Но вспомним, что эта сила получается путём математических преобразований из силы Ампера. Какой процесс описывает закон Ампера? Правильно — процесс превращения электрической энергии в механическую! То есть это тот случай, когда сила неэлектростатической природы выполняет функцию, «не имеющую никакого отношения к генерации электроэнергии» (см. Примечание выше).

Даже из попытки И. В. Савельева устранить противоречие торчат уши всё той же ошибки. Пытаясь доказать, что сила Лоренца может создавать ЭДС индукции, автор незаметно подменяет энергию магнитного поля механической энергией движения проводника. Электромагнитная индукция — это генерационный процесс. Индукционная ЭДС создаётся механической энергией, а сила Лоренца лишь «указывает направление» для движения зарядов.

Эту же ошибку (в разных вариантах) совершают и многие другие исследователи. Чтобы понять причину живучести этого феномена, обратимся к… терминологии.

Электрическая энергия

Мы ежедневно и многократно произносим слова «электрическая энергия», хотя такое понятие… не существует, по меньшей мере — в официальной электродинамике. Это скажет вам (я спрашивал!) любой физик, добросовестно усвоивший теоретический (университетский) курс электродинамики. В «Справочнике по физике» словосочетание «электрическая энергия» появляется лишь один раз в определении энергии заряженного проводника, которая, как объясняется несколькими строками ниже, «представляет собой энергию его электрического поля»². В перечне различных форм энергии, который приведен в последнем издании энциклопедического словаря «Физика»³, есть «механическая, внутренняя, химическая, ядерная…», но нет электрической энергии. В этом списке она присутствует лишь в комбинации «электромагнитная энергия».

В макромире работают два фундаментальных дистанционных взаимодействия — гравитационное и электромагнитное. Между ними есть много общего. Гравитационное взаимодействие определяет потенциальную энергию взаимодействия массивных тел — механическую энергию их взаимного расположения. Взаимной «энергией положения» обладают и два электрически заряженных тела, удерживаемых на некотором расстоянии друг от друга. Известно, что существует достаточно полная аналогия между отдельными характеристиками обоих взаимодействий (заряд — масса, напряжённость электрического поля — ускорение свободного падения и др.), да и описываются оба взаимодействия аналогичными математическими выражениями — законом всемирного тяготения и законом Кулона. Особенность электростатического взаимодействия лишь в том, что электрические заряды могут быть двух сортов. Почему массы только положительные, а электрические заряды существуют положительные и отрицательные, знает только Всевышний. Это ещё один «божий промысел», который науке ещё предстоит разгадать. Но отталкивание зарядов одного знака и притяжение зарядов противоположного знака делает потенциальную энергию положительной (отталкивание) и отрицательной (притяжение).

Любое электрически заряженное тело обладает потенциалом. Казалось бы, сам бог велел называть энергию взаимодействия заряженных тел «потенциальной электрической энергией». Но современные авторы учебников и справочников старательно избегают этого термина. Вместо этого говорят об «энергии электрического поля», плотность которой определяется квадратом электрической напряжённости. Замечание академика И. Е. Тамма, что «энергия электрического поля играет роль потенциальной энергии в смысле аналитической механики»¹ не обсуждается…

Теперь, когда мы знаем, что вихревого электрического поля не существует, можно смело утверждать, что у такого поля нет ничего, в том числе — и энергии. Но, может быть, энергия есть у разомкнутого — потенциального поля?

Понятие «электрическое поле» было предложено Фарадеем как удобная математическая модель для расчётов взаимодействия электрических зарядов. Долгое время характеристики электрического поля — напряжённость, потенциал, силовые линии, их «натяжение» и «давление» и пр. — носили абстрактный характер, представляли придумку хоть и гениального, но человеческого ума. Потребность материализовать электрическое поле появилась, когда от взаимодействия зарядов перешли к взаимодействию полей. Эта идея принадлежит Максвеллу:

Согласно старым теориям она [энергия электромагнитных явлений — К.К.] находится в электризованных телах, проводящих цепях и магнитах в форме неизвестного качества, называемого потенциальной энергией или способностью производить определённые действия на расстоянии. По нашей теории она находится в электромагнитном поле, в пространстве, окружающем наэлектризованные и намагниченные тела, а также и в этих самых телах и проявляется в двух различных формах, которые могут быть описаны без гипотез как магнитная поляризация и электрическая поляризация⁴.

В дальнейшем электрическому (и магнитному) полю приписали массу, импульс и прочие атрибуты реального физического объекта.

Согласно определению: «…потенциал численно равен потенциальной энергии, которой обладал бы (курсив мой — К.К.) в данной точке поля единичный положительный заряд»⁵. В отсутствии заряда никакой «потенциальной энергии» у электрического поля быть не может — «пустое» пространство энергией не обладает. Электрическую энергию могут иметь лишь тела, несущие электрические заряды. Если электрические потенциалы у двух тел разные, то разность потенциалов этих тел — это и есть потенциальная электрическая энергия их взаимодействия. А понятие «энергия электрического поля» — это фантом, рецидив «материализации полей».

Кроме «энергии положения» (потенциальной энергии) электрическая энергия имеет другую форму — «энергию движения». Это — энергия движущихся электрических зарядов, энергия электрического тока. Все признают, что «энергия движения» существует и обладает «некоторыми особенностями», отличающими её от потенциальной энергии, но не решаются (упаси бог!) назвать её «кинетической электрической энергией». Не будем и мы дразнить гусей и будем называть энергию движущихся зарядов «энергией движения».

Не делая никаких предположений о природе этого вида энергии, можно с большой долей уверенности утверждать, что:

1. «энергия движения» — это другая форма электрической энергии, отличная от потенциальной энергии взаимодействия неподвижных зарядов;
2. она определяется силой тока или — при движении одиночного электрического заряда — величиной заряда и его скоростью;
3. мерой «электрической энергии движения» может служить интенсивность магнитного поля, создаваемого электрическим током.

Завершая разговор об электрической энергии, необходимо сказать и об «энергии магнитного поля».

Магнитное поле (как и электрическое) — это мысленная конструкция, математическая модель для описания электродинамических взаимодействий. Но — в отличие от электрической энергии (связанной с зарядами!), — «магнитной энергии» не существует ни в какой форме. Это ещё один фантом, порожденный материализацией магнитного поля. То, что мы называем «энергией магнитного поля», можно считать лишь математическим синонимом «электрической энергии движения».

Возможно, некоторые ортодоксы сочтут эти утверждения кощунственными. К их разочарованию вынужден сознаться, что моя точка зрения (увы!) не оригинальна. Ещё в работах Э. Парселла⁶ и Р. Фейнмана⁷ показано, что поведение заряженной частицы, движущейся параллельно проводу с током, можно объяснить кулоновским взаимодействием с учётом соотношений СТО, не прибегая к понятию «магнитное поле». Аналогичные утверждения содержатся и в работах других авторов (см., например⁸). На этом основании делается вывод, что «Представление о магнитном поле есть не более чем удобный прием вычисления сил, действующих на движущиеся заряженные частицы». И, наконец: «Магнитное поле… в природе не существует… Физически реально только одно поле — электрическое».

Некоторые аргументы в пользу таких представлений даёт анализ природы электромагнитного излучения.

• Назад: Вихревое электрическое поле
• Далее: Гармонические индукционные процессы

Комментарии

Вы можете добавить свой комментарий. Пожалуйста, оставляйте только комментарии по теме данной страницы.